彭罗斯楼梯-彭罗斯楼梯解开了吗

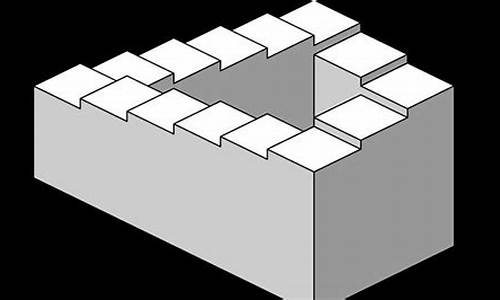
这是著名的“彭罗斯楼梯”，也叫鬼吹灯循环闭楼梯。

彭罗斯阶梯（Penrose stairs）是一个有名的几何学悖论，指的是一个始终向上或向下但却走不到头的阶梯，可以被视为彭罗斯三角形的一个变体，在此阶梯上永远无法找到最高的一点或者最低的一点。彭罗斯阶梯由英国数学家罗杰·彭罗斯及其父亲遗传学家列昂尼德·彭罗斯于1958年提出。

彭罗斯楼梯是著名的数学几何悖论之一，理论上就是，人一直沿着台阶往上走，却一直都在同一水平面打转，出现了一个无限循环的解体。我们可以发现，在彭罗斯楼梯上绝对找不出最高的一点或者是最低的一点。

彭罗斯楼梯实际上就是从基点再次回到基点的一个过程，说白了就是一个上下的过程。但是我们看到全部都是上楼梯或者下楼梯，这就是彭罗斯楼梯给我们的错觉，实际上每层楼梯的高度差都是因为阶梯的倾斜度，每阶楼梯的高度差都是大于底座坡度而引起的高度增长。

当人到达中间的时候，在上楼梯，实际上每层阶梯的高度差小于底座坡度而引起的高度增长所以你觉得你在上楼，实际上高度在下降。彭罗斯楼梯使用的就是高度差给人直观的感受。根据现实中的测试发现，只要每层阶梯有一定的倾斜度，就能够给人一种上楼梯的感觉，但实际上一直都是在水平面上。

彭罗斯阶梯不可能在三维空间内存在，但只要放入更高阶的空间，彭罗斯阶梯就可以很容易的实现。如同莫比乌斯环、克莱因瓶。

“鬼打墙”的彭罗斯阶梯是什么呢？在三维世界中，无限循环的阶梯能存在吗？

永无止尽的无限循环楼梯，叫做彭罗斯阶梯，在我国被称之为悬魂梯，也就是鬼吹灯中那个永远往下走的楼梯。

身在彭罗斯阶梯中，人们永远无法找到它的最高或最低点，也没有尽头，由英国著名数学物理学家、牛津大学数学系名誉教授彭罗斯（Roger Penrose）及其父亲提出。彭罗斯阶梯可以说是世界上有名的关于二维和三维空间的几何悖论。

彭罗斯阶梯在现实生活中是永远不可能存在的，实际上它是由我们的视觉系统瞬间意识地对一个二维图形的三维投射，形成的错视现象。虽然彭罗斯阶梯不可能在三维空间内存在，但只要放入更高阶的空间，彭罗斯阶梯就可以很容易的实现，如同莫比乌斯环、克莱因瓶。

此外，如果想要彭罗斯阶梯在现实中实现，那么必须依靠人的错觉(或者说感觉的误判)才能实现。

所需的条件：

1、“缓坡现象”和背景的光影效果：抵消人们视觉上的角度判断;

2、台阶“平面”小角度上扬：依靠小角度来抵消踝关节对于角度的判断，例如角度如果小于5度，人们是难以依靠踝关节的姿势(或者说“攀登感”)来判断它是否为水平的;

3、每个台阶必须兑现自己的落差，而不是几十个台阶来兑现一个台阶的落差;

缓坡现象原理：

当人们下一个陡坡(例如30度角)之后，再下一个中陡坡(例如只有15度)，最后换到一个小陡坡(5度)，由于对比效果，人们可能会认为在“上坡”，但是实际上却是在下坡。

这个现象在开车的时候，一些特殊山道可能会遇到，此时人们明明感觉在上坡，但空挡滑行却可能越来越快，甚至停车之后感觉车在向“上坡”方向滑行。

步行的时候这个现象通常会被

A.背景环境、

B.踝关节的姿势(或者说倾角)、

C.“攀登感”所纠正;

而构造彭罗斯阶梯(悬魂梯)的时候，可以避免上述三个纠正方式：

A.靠光影和背景来抵消环境的影响(例如墙壁上的图案本身也是歪斜的);

B.依靠小的倾角来抵消踝关节自身的角度判断(脚跟比脚尖高了10cm谁都能感觉到，但如果只有0.2cm，感觉就会很不明显，甚至完全无法发觉);

C.依靠“台阶运动”扭曲攀登感，长期的上坡或者下坡都会给自身带来比较明显的“费力”或者“省力”感，但如果只是几步的上下坡感觉就会很小，如果中间夹杂上上下台阶的动作，这个效应也会被剔除;

台阶“平面”小角度上扬

人体对于角度的感知是有不敏感区的，大角度(例如30度)，仅仅是为了保持重心，我们站上去会有明显的感觉，但小角度却难以感知。

在没有其他判定依据的前提下，人们的潜意识会认为台阶的平面是“水平”的，但恰恰是这里进行了感觉欺骗。

5度的小倾角下，tan值约为0.09，也就是说如果台阶长度是220cm，就能靠5度的倾角上扬20cm。

使用1度的倾角上扬20cm也不过就是需要不到12米而已。

最终：

1、人们需要从一个大角度的斜坡“下到”(上到)悬魂梯区域内，以兑现缓坡效应

2、每个台阶高20cm，长度要达到5米以上，以不足5度的小角度上扬每一个台阶的尽头都与上一个台阶的尽头实际上保持水平

3、利用“光影效果”给出一个与台阶平面相同倾角的壁画，并且连绵不绝

4、台阶的“下落段”必须与下一个台阶保持垂直，也就是本来应该“竖直向下”的部分也存在偏角，让两个台阶保持垂直。

扩展资料：

克莱因瓶最初由德国几何学大家菲立克斯·克莱因提出的，在1882年，著名数学家菲立克斯·克莱因发现了后来以他的名字命名的著名“瓶子”。

克莱因瓶是一个不可定向的二维紧流形，而球面或轮胎面是可定向的二维紧流形。如果观察克莱因瓶，有一点似乎令人困惑--克莱因瓶的瓶颈和瓶身是相交的，换句话说，瓶颈上的某些点和瓶壁上的某些点占据了三维空间中的同一个位置。但是事实却非如此。

事实上，克莱因瓶的瓶颈是穿过了第四维空间再和瓶底圈连起来的，并不穿过瓶壁。用扭结来打比方，如果把它看作平面上的曲线的话，那么它似乎自身相交，再一看似乎又断成了三截。但其实很容易明白，这个图形其实是三维空间中的曲线。它并不和自己相交，而是连续不断的一条曲线。

参考资料：

回魂梯是怎么弄出来的?

彭罗斯阶梯它本质上是在三维空间不可能出现的，它只有在更高一维度的空间才有可能出现的这种情况，这个彭罗斯阶梯简单的说就是人一直在走楼梯，但一直都是在原地踏步。一直都处在一个循环之中，而没有真正往上走。

这是怎么实现的呢？简单的说，它有点类似于在二维空间之中不可能出现的莫比乌斯环就是没有里面和外面的区别，怎么走它都是在外面怎么走，也都是在里面。怎么说都可以，在我们的三维世界之中，我们可以制作出莫比乌斯环，但是在三维世界之中，他有一个类似于莫比乌斯环的东西，叫做彭罗斯阶梯。这个阶梯它是采用4个顺时针方向的90度拐角所形成的一个阶梯的循环。

这个阶梯的循环就是说只要沿着这个阶梯去逆时针走，那最终人们走这个楼梯一直都是在往上走，然后一直都是往上面走的这个阶梯，却是一个循环，不可能走到更高的高度。这是为什么呢，因为这涉及到空间叠加的问题，在我们三维世界是不可能出现这样的产品的，在更高一维度的空间可以出现。因为人家已经可以把3维的世界叠加起来了，自然就能达到这样的效果，这只是一种理想之中存在的东西。

所以有很多人把这个阶梯也比作是现实之中鬼打墙的一种科学的解释，是人们误入某些更高维度的空间所出现的一种奇怪的现象，然后在一种巧合之下或者外部的干涉，或者是高维的空间生物的干涉，人们可以走出这样的空间，就回归到了正常的生活。但这种猜测其实没有绝对的科学意义并不清楚这个阶梯在更高维度的空间实现形式到底是怎样的，我们现在还不具备去实验这个东西的基础，通过设计图表现出来的也终究是不完整的，也是实现不了的。

被誉为科学界的“鬼打墙”的彭罗斯阶梯，是什么样的存在？

回魂梯在国际上又称彭罗斯阶梯(Penrose Stairs)、由莱昂内尔·彭罗斯( Lionel Penrose)和他的儿子罗杰·彭罗斯(Roger Penrose)创作。是彭罗斯三角形的一个变式。

这是一个由二维图形的形式表现出来的拥有4个90°拐角的四边形楼梯。由于它是个从不上升或下降的连续封闭循环图，所以一个人可以永远在上面走下去而不会升高。

原理方法：

假设东面为起点向南走,假设每阶楼梯落差是17厘米，我们把起点的下一阶楼梯水平面微微往上斜1厘米，这么细小的变化人在黑暗中是根本体会不到的。

那么有23阶楼梯，每阶其实都是斜一厘米的，总共往上斜了23厘米,减掉落差17 厘米，实际上人是往上走了6厘米，再换到西面，还是往上斜1厘米，走完23阶实际上又往上走了6厘米，加起来就是12厘米，再转到北面，前22阶楼梯都往上斜一厘米，最后一阶直接落在起点上。

因为起点是平的，那么实际上这一段只斜上去22-17等于5厘米，加上前面的6+6的总和12厘米正好又是17厘米，如此循环下去，永远走不完。

扩展资料：

几何悖论模型

1、莫比乌斯带

公元1858年，德国数学家莫比乌斯(Mobius，1790~1868)和约翰·李斯丁发现:把一根纸条扭转180°后，两头再粘接起来做成的纸带圈，具有魔术般的性质。

普通纸带具有两个面(即双侧曲面)，一个正面，一个反面，两个面可以涂成不同的颜色;而这样的纸带只有一个面(即单侧曲面)，一只小虫可以爬遍整个曲面而不必跨过它的边缘。这种纸带被称为"莫比乌斯带"(也就是说，它的曲面从两个减少到只有一个)。

2、克莱因瓶（Klein Bottle）

在数学领域中，克莱因瓶（Klein Bottle）是指一种无定向性的平面，比如2维平面，就没有“内部”和“外部”之分。

克莱因瓶最初的概念是由德国数学家菲利克斯·克莱因提出的。克莱因瓶和莫比乌斯带非常相像。克莱因瓶的结构非常简单，一个瓶子底部有一个洞，现在延长瓶子的颈部，并且扭曲地进入瓶子内部，然后和底部的洞相连接。

和我们平时用来喝水的杯子不一样，这个物体没有“边”，它的表面不会终结。它也不类似于气球?，一只苍蝇可以从瓶子的内部直接飞到外部而不用穿过表面（所以说它没有内外部之分）。

彭罗斯阶梯（Penrose stairs）是一个著名的代数学悖论。它是由视觉错觉所致使的一个无限循环的阶梯，并没有最高点都没有最低点，但却有爬楼梯和下楼的视觉觉得。做为一个平面构图悖论，是由于它违反大家的几何图形基本常识和物理原理，在人们的三维世界中，无限循环的阶梯是无法出现的，因为你终将抵达一个最高点或是最低点，不然大家就将可以获得一个永动发电机。

由于当物件从高空向往低健身运动时，是会释放动能的，而无尽向下的阶梯当然代表着可以无尽放会。可是，彭罗斯阶梯在视觉效果上看上去又是那样的当然，这揭露了人们视觉识别系统运行的一些与生俱来缺点或是内部结构运行体制。根据精妙的设定阶梯的宽高比，可以诱发人们视觉效果作出上坡起步或下坡路的体会，这也是画彭罗斯阶梯的重要小技巧。彭罗斯阶梯和克莱因瓶一样，都属于“不可能图形”。

它指的是那样的一种存有：如果你顺着阶梯向往上爬或向下走，在人们的理念中，只需够固执，你毫无疑问回家到一个最高点或是最低点。但在彭罗斯阶梯中，无论你是怎么往上面或向下爬，都不可能有关键，你反倒会在原地不动转，如同“鬼打墙”一样，找不着发展方向。

自然专家觉得彭罗斯阶梯基本原理是一种数字组合编号实体模型，是运用数据和感观及其参照来蒙蔽别人的一种状况，这一和小说鬼吹灯里边的悬魂梯很类似，听说在数千年前的周王朝就已经被看到而且应用，不清楚是真伪，可是彭罗斯阶梯基础理论确实十分吸引人，而鬼打墙好像可以用这一来表述。